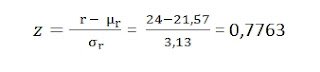Senin, 31 Oktober 2011

Uji Chi kuadrat -->> kasus dua sampel independen

fungsi :

- bila penelitian terdiri dari frekuensi-frekuensi dalam kategori diskrit
- sama dengan uji eksak fisher, hanya data disusun dalam tabel b x k , dengan b = banyak baris dan k = banyak kolom
- ekspetasi setiap sel ≥ 5

spesifikasi :

-data disusun dalam tabel kontingensi
-digunakan untuk menguji independensi



Langkah-langkah pengujian :

Ho : p(I) = p(II)
H1 : uji satu arah atau dua arah
α    : Tarafnyata

Statistik uji :

a.    JIKA DATA DISUSUN DALAM TABEL  2 x 2

1. jika ukuran sampel n < 20 maka gunakan uji eksak fisher
2. jika ukuran sampel n ≥ 20 maka gunakan uji χ² sebagai berikut :

 b. JIKA DATA DISUSUN DALAM TABEL bx k

dengan n > 40 maka gunakan uji  χ² sebagai berikut :


 
Oij : frekuensi observasi baris i dan kolom j
Eij : frekuensi ekspetasi baris i dan kolom j

Kriteria uji :

uji satu pihak = Tolak Ho jika  χ² ≥  χ²α, terima dalam hal lainnya

uji dua pihak = Tolak Ho jika  χ² ≥  χ²α/2, terima dalam hal lainnya


contoh soal :
berdasarkan standar badan telekomunikasi internasional, dengan menggunakan data ASR dari panggilan SLJJ dari kota kecil (KK) dan kota besar (KB) diperoleh hasil sebagai berikut :

STANDAR BADAN TELEKOMUNIKASI
KOTA
JUMLAH
KB
KK
SangatBaik
7
12
19
Baik
6
12
18
Buruk
0
0
0
Jelek
2
1
3
JUMLAH
15
25
40

Dengan α=5%, apakah PT. TELKOM telah mencapai World Class Operator (WCO) ?

jawab :

Ho : p(KB) = p(KK)
       PT. TELKOM telah mencapai World Class Operator (WCO) 

H1 : p(KB) ≠ p(KK)
       PT. TELKOM belum mencapai World Class Operator (WCO)

 α : 5%

 




 








              statistik uji :
 

            kriteria uji :

            α   = 5%
db       db = (b-1)(k-1)=(4-1)(2-1)=3
maka   χ²α/2  = 9,35
               
              χ² = 1,2255    <   χ²α/2  = 9,35
    a        maka Ho diterima, artinya PT. TELKOM telah mencapai World Class Operator (WCO)











                  sumber : Buku pegangan metode statistika Non -parametrik jurusan statistika FMIPA UNPAD ^,^
  

 
di 2 komentar:

Kamis, 13 Oktober 2011

Uji Eksak Fisher --->> kasus dua sampel independen



          Fisher test merupakan uji eksak yang diturunkan oleh seorang bernama Fisher, karenanya disebut uji eksak Fisher. Uji ini dilakukan untuk menguji signifikansi hipotesis komparatif dua sampel independen. Perbedaan uji fisher dengan uji chi square adalah pada sifat kedua uji tersebut dan ukuran sampel yang diperlakukan. Uji fisher bersifat eksak sedangkan uji chi square bersifat pendekatan. Uji chi square dilakukan pada data dengan sampel besar, sedangkan uji Fisher dilakukan pada data dengan sampel kecil. Data yang dapat diuji dengan fisher test ini berbentuk nominal dengan ukuran sampel n sekitar 40 atau kurang, dan ada sel-sel berisikan frekuensi diharapkan kurang dari lima. Perhitungan Fisher Test sama sekali tidak melibatkan chi-square, akan tetapi langsung menggunakan peluang.

Fungsi :
untuk menguji apakah ada perbedaan dua perlakuan yang mungkin dari dua populasi

spesifikasi :
skala ukur nominal atau ordinal
data disusun dalam tabel kontingensi 2 x 2
ukuran sampel n ≤ 20



Langkah pengujian:
Ho       :  p(I)=p(II)
H1       : satu arah atau dua arah
α          : 5%
susun data dalam tabel kontingensi 2 x 2 sebagai berikut:
-
+

Kelompok I
A
B
A+B
Kelompok II
C
D
C+D

A+C
B+D
N

Statistik uji :

kriteria uji :
Tolak H0  jika p ≤ α (satu arah) atau p ≤ α/2 (dua arah), terima dalam hal lainnya.

 Catatan:
Untuk menghindari penyimpangan yang lebih ekstrim yang mungkin terjadi, harus dihitung pula peluang-peluang dengan membuat tabel baru, dimana jumlah marjinalnya tetap, dan nilai terkecil dari salah satu sel berkurang sampai dengan 0.

contoh soal :

sebuah pertanyaan dilontarkan kepada bebo toh sepak bola dan bukan bebotoh sepak bola. apakah setuju dengan pembubaran PSSI

Bebotoh
Bukan Bebotoh
S
TS
S
S
S
TS
TS
TS
TS
TS
S

TS





Apakah terdapat perbedaan jawaban yang signifikan?

Jawab:

H0        :  pB = pBB (tidak ada perbedaan yang signifikan)
H1        :  pB ≠ pBB (ada perbedaan yang signifikan)
α          :  5%
B
BB

S
4
1
5
TS
3
4
7

7
5
12


Statistik uji :


Kriteria uji:
Tolah Ho jika p≤ α/2, terima dalam hal lainnya. Ternyata p =1,33 > α/2= 0,025. Jadi Ho diterima artinya  tidak ada perbedaan yang signifikan.


Jika dipertimbangkan penyimpangan-penyimpangan yang lebih ekstrim dibuat tabel sebagai berikut:
B
BB

S
5
0
5
TS
2
5
7

7
5
12


Statistik uji :










Jadi kemungkinan yang lebih ekstrim adalah :

P          =   p1 + p2
            =  1,33 + 0,2917
            =  1,6217

kesimpulan : Ho diterima pada p = 1,6217












sumber : dari buku statistika non parametrik jurusan statistika FMIPA UNPAD ^^


di 2 komentar:

Jumat, 07 Oktober 2011

Uji Deret = Uji Runtun = Run Test ---->> kasus satu sampel

Fungsi : menguji sederetan data yang terdiri atas dua kategori apakah tersusun secara random atau sistematik


Runtun didefinisikan sebagai suatu urutan lambang-lambang yang sama, yang diikuti serta mengikuti lambang-lambang yang berbeda.



Contoh :


+ + +  - -  +  - -  + +  - - -   + + +  - - - -  + + + + +  - 
    1      2   3   4    5      6        7         8           9        10

Ada 10 runtun = r ,  tanda + = n1 ,  tanda - = n2
Langkah-langkah pengujian:

H0 : data tersusun random
H1 : data tidak random/sistematis  (dua arah)
α    : taraf nyata

a. Jika Ukuran Sampel Kecil yaitu  dan  ≤ 20

Statistik Uji : hitung banyaknya runtun = r
Gunakan tabel F1 dan F2 (Tabel 8)

Tabel F1 : nilai-nilai batas terkecil r untuk menolak H0
Tabel F2 : nilai-nilai batas terbesar r untuk menolak H0

Kesimpulan :
jika r berada antara  F1 dan F2 maka terima H0 dan jika r < F1 atau r > F2 maka tolak H0

Contoh soal :

Dalam suatu kantin diperusahaan elektronika, terdapat sekelompok karyawan wanita yang sedang makan siang. Dari sekelompok karyawan itu ada 18 orang diambil secara random, selanjut diwawancarai, kapan akan mengambil cuti hamil. Dalam pertanyaan itu disediakan dua alternative jawaban yaitu akan mengambil cuti besar sebelum melahirkan atau sesudah melahirkan. Wawancara dilakukan secara berurutan, yaitu mulai dari No.1 dan berakhir No.18. 

Diperolehkan data “Waktu pengambilan cuti besar Karyawati”, yaitu 

No
Jawaban
1
1
2
1
3
0
4
1
5
0
6
1
7
0
8
0
9
1
10
1
11
0
12
0
13
0
14
1
15
1
16
0
17
1
18
0

Keterangan :
1 = (+) : mengambil cuti besar sebelum  melahirkan
0 = (-) mengambil cuti besar sesudah melahirkan

Apakah data diatas tersusun random?

Berdasarkan hal tersebut diatas maka dilakukan pengujian:

Jawab :

H0 : data tersusun random
H1 : data tidak random
α    :    5%

Dari data diperoleh:








Maka :
r  =  banyak runtun =  12
gunakan tabel  F1 dan F2 untuk menentukan harga kritis dalam uji runtun
dengan α = 5%

untuk batas terkecil r untuk menolak  H0
 F1 =4


Untuk batas terbesar r untuk menolak H0
 F2 = 14

·   
dcj   Kriteria uji:

jika r berada antara  F1 dan F2 maka terima H0 dan jika r < F1 atau r > F2 maka tolak H0
karena  F1  = 14 dan  F2  = 14 maka r berada diantara F1 dan F2, sehingga H0 diterima
artinya data tersebut disusun secara random.     

b.Jika Ukuran Sampel besar yaitu  dan  ≥  20

 
       
 

 
Kriteria Uji :
Tolak H0  jika -zα/2 > zhitung > zα/2 , terima dalam hal lainya.
(Gunakan Tabel 1), atau jika p ≤ α/2 maka H0 ditolak, terima dalam hal lainnya.


Contoh soal :

Suatu penelitian tentang sanitasi rumah telah dilakukan.Diambil sebanyak 42 rumah.Masing-masing rumah diukur kelembaban udaranya didapatkan data urutan sampel berdasarkan kelembaban pada tabel dibawah.Selidikilah dengan α = 10 %, apakah sampel rumah tersebut random (acak) berdasarkan kelembabannya.



Nomor
Kelembaban Rumah
Nomor
Kelembaban Rumah
1
68
22
59
2
56
23
48
3
78
24
53
4
60
25
63
5
70
26
60
6
72
27
62
7
65
28
51
8
55
29
58
9
60
30
68
10
64
31
65
11
48
32
54
12
52
33
79
13
66
34
58
14
59
35
70
15
75
36
59
16
64
37
60
17
53
38
55
18
54
39
54
19
62
40
60
20
68
41
54
21
70
42
50


Jawab :


H0 : tidak beda dengan random
H1 : ada beda dengan random
α   : 10 %

Statistik Uji :


n ≤ 60   = ( - ),  n > 60 = ( + )


No
Kelembaban Rumah
Tanda
No
Kelembaban Rumah
Tanda
1
68
+
22
59
-
2
56
-
23
48
-
3
78
+
24
53
-
4
60
-
25
63
+
5
70
+
26
60
-
6
72
+
27
62
+
7
65
+
28
51
-
8
55
-
29
58
-
9
60
-
30
68
+
10
64
+
31
65
+
11
48
-
32
54
-
12
52
-
33
79
+
13
66
+
34
58
-
14
59
-
35
70
+
15
75
+
36
59
-
16
64
+
37
60
-
17
53
-
38
55
-
18
54
-
39
54
-
19
62
+
40
60
-
20
68
+
41
54
-
21
70
+
42
50
-






n1 = 24
n2 = 18
r    = 24





           
    










Kriteria Uji :
Tolak H0  jika -zα/2 > zhitung > zα/2 , terima dalam hal lainya.
(Gunakan Tabel 1/ tabel distribusi normal standart), atau jika p ≤ α/2 maka H0 ditolak, terima dalam hal lainnya.
Dengan α = 0,1 ,uji dua sisi α/2 = 0,05 maka diperoleh zα/2 = 1,65

Karena | 0,7763 | < 1,65 sehingga H0 diterima, Berarti sampel rumah tersebut random (acak) berdasarkan kelembabannya.















Sumber : http://www.scribd.com/doc/19759534/Statistik-Run-Test-Satu-Sampel 
dan buku pegangan Metode Statistika TakParametrik oleh statistika FMIPA UNPAD.

^,^ 

di Tidak ada komentar:
Langganan: Postingan (Atom)